qchisq(0.95,20)Final term
1.
모수 \(\theta\)에 대한 서로 독립인 비편향 추정량 \(\hat{\theta}_1\)과 \(\hat{\theta}_2\)이 존재하며 \(Var(\hat{\theta}_i) = \sigma^2_i, i=1,2\)이라고 한다. 이를 이용하여 새로운 추정량 \(\hat{\theta}_{a_1,a_2} = a_1\hat{\theta}_1 + a_2\hat{\theta}_2\)를 정의할 때 다음에 답하시오.
(a)
\(\hat{\theta}_{a_1,a_2}\)이 비편향추정량이 될 \(a_1\)과 \(a_2\)의 조건을 구하시오
answer
비편향 추정량 \(\theta_1\), \(\theta_2\), \(E(\hat{\theta}_1) = \bar{\theta}\), \(E(\hat{\theta}_2) = \bar{\theta}\)
\(E(\hat{\theta}_{a_1,a_2}) = E(a_1\hat{\theta}_1 + a_2\hat{\theta}_2) = a_1E(\hat{\theta}_1) + a_2E(\hat{\theta}_2) = a_1\bar{\theta} + a_2\bar{\theta} = \bar{\theta}(a_1 + a_2)\)
\(\bar{\theta} = \bar{\theta}(a_1 + a_2)\), 즉, \(a_1 + a_2 = 1\)
(b)
비편향추정량인 \(\hat{\theta}_{a_1,a_2}\) 중에서 가장 작은 분산을 가지는 추정량을 구하시오.
answer
\(Var(\hat{\theta}_1) = \sigma^2_1\), \(Var(\hat{\theta}_2) = \sigma^2_2\)
\(Var(\hat{\theta}_{a_1,a_2}) = Var((a_1 + a_2)\bar{\theta}) = (a_1 + a_2)^2 Var(\hat{\theta})\)
\((a_1 + a_2)^2\)이 최소이면서 \(a_1 + a_2=1\)일 때, 즉 \(a_1 = 0.5, a_2 = 0.5\)일 때 가장 작은 분산을 가진다.
2.
\(X_1,X_2,\dots,X_n\)이 \(Ber(p)\)로부터의 랜덤표본이라고 하자. 모집단의 분포 \(Ber(p)\)의 분산인 \(p(1-p)\)을 추정하고자 한다.
(a)
\(p(1-p)\)에 대한 비편향추정량의 크래머-라오 하한값을 구하시오.
answer
bias = \(E(\hat{p}(1-\hat{p})) - p(1-p) = 0\)
\(E(\bar{X}) = np\), \(Var(\bar{X}) = np(1-p)\)
\(E(\hat{p}(1-\hat{p})) = E(\frac{\bar{X}}{n}(1-\frac{\bar{X}}{n})) = E(\frac{\bar{X}}{n} - (\frac{\bar{X}}{n})^2) = p - p^2\)
\(f(x) = p^x(1-p)^{1-x}\)
\(logf(x) = xlogp + (1-x)log(1-p)\)
\(\frac{\partial log f(x)}{\partial p} = \frac{x}{p} - \frac{1-x}{1-p}\)
\(\frac{\partial^2 log f(x)}{\partial^2 p} = -\frac{x}{p^2} - \frac{1-x}{(1-p)^2}\)
\(\star I(\theta) = E[(\frac{\partial}{\partial \theta} log f(C; \theta))^2)]\)
\(I(p) = -E(-\frac{x}{p^2}-\frac{1-x}{(1-p)^2}) = \frac{1}{p} + \frac{1}{1-p} = \frac{1}{p(1-p)}\)
\(CRLB = \frac{g'(p)^2}{nI(p)} = \frac{(1-2p)^2p(1-p)}{n}\)
\(\star g(p) = p(1-p)\), \(g'(p) = 1-2p\)
(b)
\(X_1(1-X_2)\)의 기댓값을 구하시오.
answer
\(E(X_1(1-X_2)) = E(X_1 - X_1X_2) = E(X_1) - E(X_1X_2) = E(X_1) - E(X_1)E(X_2) = p - p^2 = p(1- p)\)
(c)
\(p(1-p)\)에 대한 최소분산 비편향 추정량을 구하시오.
answer
\(E(\bar{X}_n(1 - \bar{X}_n)) = \frac{(n-1)p(1-p)}{n}\)
\(p(1-p) = \frac{n\bar{X}_n(1-\bar{X}_n)}{n-1}\)
(d)
\(p(1-p)\)에 대한 적률추정량을 구하시오.
answer
\(M_1 = E(\bar{X}) = p\)
\(M_2 = Var(\bar{X}) + E(\bar{X})^2 = p(1-p) + p^2 = p\)
\(p(1-p)\)의 적률추정량 \((p(1-p))^{MME} = M_2 - M^2_1 = p - p^2 = p(1-p)\)
(e)
\(p(1-p)\)에 대한 최대가능도추정량을 구하시오.
answer
\(f(x) = p^x(1-p)^{1-x}, x=0,1, 0<p<1\)
\(L(p) = f(x_1|p)\dots f(x_n|p) = p^{x_1}(1-p)^{1-x_1}\dots p^{x_n}(1-p)^{1-x_n} = p^{\sum x_i}(1-p)^{n-\sum x_i}\)
\(l(p) = \sum x_i log p + (n-\sum x_i) log (1-p)\)
\(l'(p) = \frac{\sum x_i}{p} - \frac{n-\sum x_i}{1-p} = 0\)
\(\hat{p} = \frac{\sum x_i}{n} = \bar{X}\)
\((\hat{p}(1-\hat{p}))^{MLE} = \bar{X}(1-\bar{X})\)
3.
다음 분포를 따르는
\[f(x;\theta) = \theta exp (-\theta x) I (x>0)\]
모집단으로부터의 랜덤표본 \(X_1,\dots,X_n\)을 이용하여 \(\theta\)에 대한 신뢰구간을 구하고, 다음 가설
\[H_0 : \theta = 2 \text{ vs } H_1 : \theta \neq 2\]
을 검정하고자 한다. 다음에 답하시오.
(a)
\(\theta\)에 대한 적절한 추축변량을 구하고, 해당 추축변량의 분포를 명시하시오.
answer
\(X_i \sim exp(\frac{1}{\theta})\)
\(2X_i \theta \sim exp(2)\)
\(2n\bar{X}\theta \sim \chi^2 (2n)\)
(b)
\(\theta\)에 대한 95%신뢰구간을 구하시오.
answer
\((\chi^2_{0.025} (2n) \le 2n \bar{X} \theta \le \chi^2_{0.975} (2n)) = 0.95\)
\(\theta_{0.95} \to (\frac{\chi^2_{0.025}(2n)}{2n\bar{X}} , \frac{\chi^2_{0.975}(2n)}{2n\bar{X}})\)
(c)
\(P(X>1)\)에 대한 95% 신뢰구간을 구하시오.
answer
\(P(X>1) = \int^{\infty}_1 \theta e^{-x\theta} dx = [ e^{x\theta}]^{\infty}_1 = e^{-\theta}\)
\(P(X>1)\) \(95\)% CI : \((exp(\frac{\chi^2_{0.9755}(2n)}{2n\bar{X}} , exp(\frac{\chi^2_{0.025}(2n)}{2n\bar{X}}))\)
(d)
가설에서 고려하고 있는 \(\theta\)의 전체 모수공간 \(\Omega\)와 귀무가설 하에서의 모수공간 \(\Omega_0\)을 구하시오.
answer
\(\Omega = \{ \theta : \theta > 0 \}\)
\(\Omega_0 = \{ \theta: \theta = 2\}\)
(e)
\(\theta\)의 가능도 함수를 기술하시오.
answer
\(L(\theta) = \theta^n e^{-\theta n \bar{X}}\)
(f)
\(\theta\)의 \(\Omega\)에서의 최대가능도 추정량과 \(\Omega_0\)에서의 최대가능도 추정량을 구하시오.
answer
\(\hat{\theta}^{\Omega} = \frac{1}{\bar{X}}\)
\(\hat{\theta}^{\Omega_0} = 2\)
(g)
일반화 가능도 비 \(\Lambda\)을 구하시오.
answer
\(\frac{L(\hat{\theta}^{\Omega_0})}{L(\hat{\theta}^{\Omega})} = \frac{\hat{\theta}^{n,\Omega_0} e^{-\hat{\theta} n \bar{X}}}{\hat{\theta}^{n,\Omega} e^{-\hat{\theta} n \bar{X}}} = (\frac{2}{n})^2 e^{n\bar{x}(\theta-2)}\)
(h)
유의수준 \(\alpha\)인 가능도비 검정법의 기각역을 \(\chi^2\)분포의 분위수를 사용하여 표현하시오.
answer
7장 예제 7.2.3. 참고
\(2(l(\hat{\theta}^{\Omega}) - l(\hat{\theta}^{\Omega_0})) = 2n(\bar{x}\theta_0 - 1 -log(\bar{X}\theta_0))\)
최대가능도비 검정의 기각역 형태 \(2n(\bar{x}\theta_0 - 1 -log(\bar{X}\theta_0))\ge c\)
기각역
\(\begin{cases} \bar{x}\theta_0 \le c_1 \text{ 또는 } \bar{x}\theta_0\ge c_2 \\ c_1 log c_1 = c_2 - log c_2\end{cases}\)
4.
확률밀도한수가
\[f(x;\theta) = \frac{1}{\theta} I (0\le x \le \theta)\]
인 분포로부터 하나의 관찰값 \(X\)를 얻었다. 이 때 가설
\[H_0 : \theta = 1 \text{ vs } H_1 : \theta = 2\]
에 대한 기각역을 \(C = \{x:x>0.8\}\)로 했을 때 제1종오류를 범할 확률과 검정력을 계산하시오.
answer
\(\alpha = P(\text{Reject } H_0 | H_0 \text{True})\)
\(\alpha = P(x>0.8 | \theta = 1)\)
\(= \int^1_{0.8} 1 dx = [ x ]^1_{0.8} = 1-0.8 = 0.2\)
\(\beta = P(\text{type 2 Error}) = P(\text{Not Reject } H_0 | H_0 \text{ False})\)
\(P(x<0.8 | \theta = 2)\)
\(= \int^{0.8}_0 \frac{1}{2} dx = [\frac{1}{2} x]^{0.8}_0 = \frac{0.8}{2} - \frac{0}{2} = \frac{0.8}{2} = 0.4\)
\(\therefore\) 검정력 :\(1-\beta = 0.6\)
5.
\(X_1, \dots,X_n\)을 \(N(0,\sigma^2)\)으로부터의 랜덤표본이라고 하자
(a)
가설 \(H_0:\sigma^2 = 4\) vs \(H_1: \sigma^2 = 9\)에 대한 최강력 검정의 기각역은
\[C = \{ (x_1,\dots,x_n):\sum^n_{i=1}x_i^2 \ge c\}\]
의 꼴로 주어짐을 보이시오.
answer
\(L(\sigma^2) = \Pi^n_{i=1} f(x_2 : \sigma^2) = \Pi^n_{i=1} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x_i^2}{2\sigma^2}} * \mu=0\)
\(= (\frac{1}{2\pi\sigma^2})^{\frac{n}{2}} e^{-\frac{\sum^n_{i=1}x_i^2}{2\sigma^2}}\)
네이만 피어슨 정의에 의하면, \(LR = \frac{L(H_0)}{L(H_1)} = \frac{L(4)}{L(9)} \le k\)
\(LR = \frac{L(4)}{L(9)} = \frac{(\frac{1}{2\pi 4})^{\frac{n}{2}} e^{-\frac{\sum^n_{i=1} x_i^2}{2 \times 4}}}{(\frac{1}{2\pi 9})^{\frac{n}{2}} e^{-\frac{\sum^n_{i=1} x_i^2}{2 \times 9}}}\)
\(= (\frac{9}{4})^{\frac{n}{2}}e^{-\sum^n_{i=1}x^2_i(\frac{1}{8}-\frac{1}{18})}\)
\(= (\frac{9}{4})^{\frac{n}{2}}e^{-\frac{5}{72}\sum^n_{i=1}x^2_i} \le k\)
\(\to e^{-\frac{5}{72}\sum^n_{i=1}x^2_i} \le k\)
\(\to -\frac{5}{72}\sum^n_{i=1}x^2_i \le k\)
\(\to \sum^n_{i=1}x^2_i \ge k\)
기각역: \(\therefore c = \{ (x_1, \dots ,x_n) : \sum^n_{i=1} x^2_i \ge c)\)
(b)
표본의 크기가 \(n=20\)일 때 유의수준이 \(\alpha=0.05\)이기 위한 상수 \(c\)의 값을 \(\chi^2\)분포의 분위수를 사용하여 표현하시오.
answer
\(\alpha = P(\text{Reject } H_0 | H_0 \text{True})\)
\(= P(\sum^n_{i=1}x^2_i \ge k | \sigma^2 = 4)\)
\(= P(\sum^n_{i=1}\frac{\chi^2_i}{\sigma^2} \ge \frac{k}{\sigma^2}|\sigma^2 = 4)\)
\(= P(\sum^{20}_{i=1} \frac{\chi^2_i}{4} \ge \frac{k}{4} | \sigma^2 = 4)\)
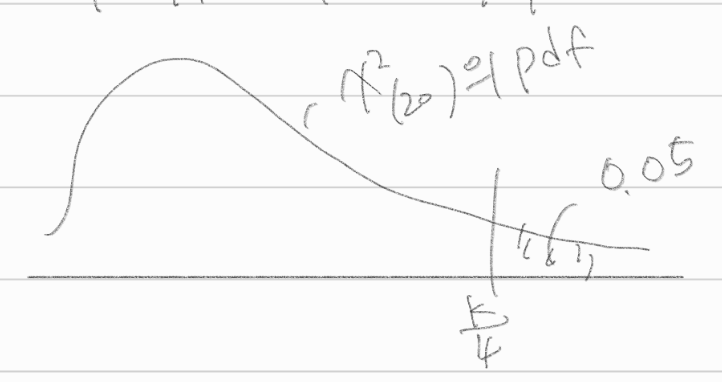
\(\frac{k}{4} = \chi^2_{0.05(20)}\)
round(4*qchisq(0.95,20),2)\(k = 4\chi^2_{0.05(20)} = 125.64\)
\(c = \{(x_1,\dots,x_n) : \sum^n_{i=1}\ge 125.64\}\)
(c)
표본의 크기가 \(n=20\)일 때 (b)에서 찾은 기각역에 대한 제2종오류를 범할 확률을 구하시오.
answer
\(\beta = P(\text{Not Reject } H_0 | H_1 \text{True})\)
\(= P(\sum^n_{i=1}x^2_i \le k | \sigma^2 = 9)\)
\(\star\)
모집단 분포 \(X_i \sim N(0,\sigma^2)\)
표준화 \(\frac{X_i}{\sigma} \sim N(0,1)\)
표분화 제곱 분포는 카이제곱 \((\frac{X_i^2}{\sigma})^2 \sim \chi^2_1, i=1,2,\dots, n\)
카이제곱의 합의 자유도 합 \(\sum^n_{i=1}(\frac{X_i}{\sigma})^2 \sim \chi^2_{(n)}\)
\(\star\)
\(= P(\sum^n_{i=1}\frac{\chi^2_i}{\sigma^2} \le \frac{k}{\sigma^2}|\sigma^2 = 9)\)
\(= P(\sum^{20}_{i=1} \frac{\chi^2_i}{9} \le \frac{k}{9} | \sigma^2 = 9)\)
\(\frac{k}{9} = \chi^2_{0.05(20)}\)
qchisq(0.95,20)round(9*qchisq(0.95,20),2)\(k = 9\chi^2_{0.05(20)} = 282.69\)
\(c = \{(x_1,\dots,x_n) : \sum^n_{i=1}\le 282.69\}\)
랜덤표본\(X_1,X_2,\dots,X_n\)의 분포가 확률밀도함수 \(f(x;\theta), \theta\in\Omega\)를 따른다고 하자. 이때 표본과 모수 \(\theta\)의 함수인 확률변량 \(T(X_1,X_2,\dots, X_n;\theta)\)의 분포가 모수 \(\theta\)에 의존하지 않으면 이를 추축변량이라 한다.
6.
\(X_1,X_2,\dots,X_n\)이 \(N(\mu,\sigma^2)\)로부터 얻은 랜덤표본이라고 하자. 모평균 \(\mu\)가 알려져 있지 않은 경우 \(H_0 : \sigma^2 = 4\) vs \(H_1 : \sigma^2 \neq 4\)을 검정하고자 한다.
(a)
적절한 추축변량을 이용하여 \(\sigma^2\)에 대한 \(100(1-\alpha)%\) 신뢰구간을 구하시오.
answer
\(\frac{\sum(X_i - \bar{X})2}{\sigma^2} = \frac{(n-1)S^2}{\sigma^2} \sim \chi_{(n-1)}^2\)
\(P[\chi_L \le \frac{(n-1)S^2}{\sigma^2} \le \chi_U] = 1-\alpha\)
\(P[\chi_{\alpha/2} \le \frac{(n-1)S^2}{\sigma^2} \le \chi_{1-\alpha/2}] = 1-\alpha\)
\(P[\frac{(n-1)S^2}{\chi^2_{1-\alpha/2}} \le \sigma^2 \le \frac{(n-1)S^2}{\chi^2_{\alpha/2}}] = 1-\alpha\)
\(\therefore (\frac{(n-1)S^2}{\chi^2_{\alpha/2}},\frac{(n-1)S^2}{\chi^2_{1-\alpha/2}})\)
(b)
유의수준 \(\alpha\)인 일반화 가능도비 검정 기각역을 구하시오.
answer
모평균 \(\mu\)의 최대가능도 추정량은 가설에 관계없이 언제나 \(\bar{X}\)
모분산 \(\sigma^2\)의 최대가능도 추정량은 귀무가설 하에서는 \(4\)이며, 전체 모수공간\(\Omega\)내에서는 \(\hat{\sigma}^2 = \frac{\sum^n_{i=1}(X - \bar{X})^2}{n}\)
일반화 가능도비 \(\Lambda(X_1,X_2,\dots,X_n) = (\frac{\sum^n_{i=1} (X_i - \bar{X}_n)^2}{4n})^{n/2} \times exp[-\frac{1}{2} \{ \frac{\sum^n_{i=1}\{(X_i - \bar{X}_i)}{4} \}^2 + \frac{n}{2}]\)
\(= (\frac{\hat{\sigma}^2}{4})^{n/2} exp\{ -(\frac{n}{2})(\frac{\hat{\sigma^2}}{4}) + \frac{n}{2} \}\)
\(\Lambda = \frac{\hat{\sigma}^2}{4}^{n/2} exp(-\frac{n}{2}\frac{\hat{\sigma}^2}{4} + \frac{n}{2})\)
\(\frac{\hat{\sigma}^2}{4} exp(-\frac{\hat{\sigma}^2}{4}) \le (\lambda^*)^{2/n} exp(-1) = c^*\)
\(\frac{\hat{\sigma}^2}{4}<1\)일 때는 단조증가, \(\frac{\hat{\sigma}^2}{4}>1\)일 때는 단조감소
기각영역 ; \(C = \{ (x_1,x_2,\dots,x_n):(\frac{\hat{\sigma}^2}{4} \le a\) 또는 \(\frac{\hat{\sigma}^2}{4} \ge b \}\)
\(n\frac{\hat{\sigma}^2}{4} = \frac{\sum^n_{i=1}(X_i - \bar{X}_n)^2}{4} \sim \chi^2(n-1)\)
\(P[\frac{\sum^n_{i=1}(X_i - \bar{X}_n)^2}{4} \le \chi^2_{1-\alpha/2}(n-1)|H_0]\)
\(= P[\frac{\sum^n_{i=1}(X_i - \bar{X}_n)^2}{4} \ge \chi^2_{\alpha/2}(n-1)|H_0]\)
\(= \frac{\alpha}{2}\)
그러므로 카이제곱분포의 양쪽꼬리에서 \(\alpha/2\)씩 고려한 일반화 가능도비 검정법의 근사꼴로서 기각영역은
\(\frac{\sum^n_{i=1}(X_i - \bar{X}_n)^2}{4} \le \chi^2_{1-\alpha/2}(n-1)\)
또는 \(\frac{\sum^n_{i=1}(X_i - \bar{X}_n)^2}{4} \ge \chi^2_{\alpha/2}(n-1)\)
(c)
\(n=10\)이고 표본분산 \(S^2\)의 관측값은 \(6\)이라고 한다. (b)의 일반화 가능도비 검정법으로 유의확률 (\(p-value\))을 구하시오.
answer
1-pchisq(6/4*9,9)